
Powszechnie znany jest Grasshopper, coś słyszeliśmy o Generative Components. Temu ostatniemu należy się przyjrzeć z niejednego powodu. Najważniejsze to filozofia programu, zasługująca na zauważenie. Artykuł zawiera wskazówki dla początkujących. Istnieje pewien umowny, pozornie żartobliwy, podział programów komputerowych wykorzystywanych w inżynierii i architekturze: przygotowane dla inżynierów oraz przygotowane przez nich. Te pierwsze są przyjazne użytkownikowi oraz prawie uniwersalne. Te drugie realizują postawione zadania, ignorując poziom ich przystępności.
Te pierwsze trafiają do szerokiego grona użytkowników, te drugie są tworzone zwykle pod konkretne zamówienie. Istotą pierwszych jest metoda, istotą drugich – cel. Pierwsze są powszechnie znane, o drugich coś słyszeliśmy. Znane są AutoCAD oraz ArchiCAD i Revit (jako narzędzia BiM). O Microstation co najmniej słyszeliśmy lub go używamy. Jednak niewiele wiemy o oprogramowaniu powstałym np. w celu realizacji wizji Franka Ghery, a nazwa mówi sama za siebie: Ghery Technologies. W dziedzinie parametrycznego programowania jest w gruncie rzeczy podobnie. Powszechnie znany jest Grasshopper, a coś słyszeliśmy o Generative Components. Temu ostatniemu należy się przyjrzeć z niejednego powodu. Najważniejszy to filozofia programu, zasługująca na zauważenie.
GC czy Grasshopper?
Zdaję sobie sprawę z przekłamania zaproponowanego podziału na „programy tworzone dla” i „programy tworzone przez”. Przy powstawaniu specjalistycznego oprogramowania praktycznie zawsze wykorzystywana jest bowiem unikalna wiedza branży, do której jest ono adresowane. Czy jednak architekt za najlepszy program uzna ten, który stworzy sam dla siebie? W założeniach tak, ale w realizacji już niekoniecznie. Istnieje bowiem pewien próg wyznaczony np. przyjaznością interfejsu użytkownika. To kryterium wpłynęło między innymi na popularność Grasshopper (GH) i niszową znajomość Generative Components (GC). Wyznacza ono pierwszą, najbardziej zauważalną różnicę obu programów. Język skryptowy GH ma postać wizualną, graficzną, natomiast GC posługuje się niemal tekstowym językiem skryptowym. Interfejs bardziej przypomina okna dialogowe języków programowania (np. Visul Basic) niż program graficzny – twórcy, programując narzędzie, myśleli o celach, jakie ma zrealizować, a zapomnieli o przystępności metod – programując GC, nadali „programistyczny” charakter interfejsu, bo był im znany i dla nich przystępny, a zapomnieli o użytkowniku. Kolejne wersje GC starają się choć trochę naśladować użytkową przystępność Grasshoppera. Zatem plus dla GH? Niekoniecznie. Grasshopper to zbiór dynamicznych bibliotek DLL (Dynamic Link Library) podczas gdy Generative Components oferuje w pełni otwartą architekturę, dokładnie taką jak zorientowane obiektowo języki programowania wysokiego poziomu. Innymi słowy, w GH dostępnych narzędzi i metod jest dokładnie tyle, ile przewidziano i przygotowano w dynamicznych bibliotekach, a GC takiego ograniczenia nie ma.
Druga podstawowa różnica pomiędzy aplikacjami polega na tym, że GH występuje wyłącznie jako plug-in do programu Rhinoceros, podczas gdy GC występuje również w postaci niezależnego programu, tzw. stand-alone application, czyli nie wymaga zainstalowania jakiegokolwiek dodatkowego programu – środowiska pracy. Zatem plus dla GC? Również – niekoniecznie. Tylko przez krótki czas zainteresowane osoby mogły pobrać z internetu tę wersję GC bez przesadnych procedur rejestracyjnych. Dziś Bentley oferuje np. studentom wprawdzie swobodny (darmowy) dostęp do całej gamy swoich programów, ale w procedurze rejestracji należy podać „kod uczelni”. Metoda wprawdzie weryfikuje, czy osoba ma status studenta, ale też potrafi skutecznie zniechęcić do poszukiwania kodu szkoły. Warto jednak o ten kod zapytać uczelniany lub wydziałowy zespół IT, jako że GC to narzędzie potężne i stosunkowo łatwe do opanowania, o ile wczytamy się w jego żelazną logikę i uwolnimy od myślenia dotychczasowymi stereotypami.
Trzecia różnica pomiędzy GC i GH wystąpi rzadko. Wśród użytkowników obu programów będą tacy, którzy potrafią napisać narzędzia do AutoCAD (np. w Autolisp) czy stworzyć nowe komendy do Revit (w VBNet lub C#). Ci użytkownicy GH, którzy rozpoczną pokonywanie jego ograniczeń poprzez pisanie własnych procedur, w rezultacie zupełnie go pominą programując własne plug-in do Rhino. Natomiast użytkownicy GC docenią wówczas „zorientowane obiektowo”, programistyczne środowisko programu.
W porównaniach obu programów warto również odwołać się do autorytetów. Zarówno Lars Hesselgren, autor: Elements of Parametric Design, jak i Hugh Whitehead, szef specjalistów modelowania w firmie Foster & Partners, wskazują, że należy znać oba programy, bo tylko w ten sposób można dobrać odpowiednie narzędzie. Obaj wskazują, że najistotniejszy jest cel, który zamierzamy zrealizować, problem, który chcemy rozwiązać. Znając cel, poszukujemy narzędzia jego realizacji. Nie odnajdując tego narzędzia wśród oferowanych, w skrajnej sytuacji tworzymy je sami – taką tezę stawiają. Panowie przewidują również, że w praktyce dojdzie do swoistej unifikacji obu narzędzi dzięki „podpatrywaniu” konkurencji, choć domniemują, że lidera jak zwykle wykreuje rynek spośród największych developerów oprogramowania, do których należy między innymi Autodesk, co może skutkować (i skutkuje) pojawieniem się konkurencyjnych programów, w szczególności zintegrowanych z technologią BiM. W tym kontekście obaj bardzo podkreślają pozytywnie politykę firmy McNeel, polegającą na otwartym dostępie do Rhino i konsekwentnym promowaniu wszelkiego typu plug-in do niego. Pointa jest oczywista i została właśnie wypowiedziana. Warto znać oba programy, za chwilę mogą się bowiem pojawić trzeci i czwarty, które opanujemy łatwiej dzięki temu, że będziemy znać i rozumieć pierwowzory. Przede wszystkim jednak zapamiętajmy tę myśl, że najistotniejszy jest cel, problem, którego rozwiązania poszukujemy. Poświęcamy uwagę Generative Components i jego szczególnym cechom, by rozpoznać, czy jest narzędziem, które możemy zastosować do realizacji zadań jakie przed nami stoją lub zostaną postawione. Dlatego musimy poznać program, choćby w ogólnym zarysie.
Postać modelu w Generative Components
Jako architekci jesteśmy przyzwyczajeni do budowania trójwymiarowych modeli w wirtualnym świecie komputera. Trójwymiarowy obiekt może być budowany powierzchniami lub modelowany bryłowo. Znają tę technikę użytkownicy zarówno AutoCAD, jak i 3DMAX, Rhino oraz wielu innych programów. Użytkownicy Revit lub ArchiCAD posługują się obiektami zaawansowanymi, ale geometria zapamiętywana jest na podobnej zasadzie – każdy z elementów składowych ma swoje odzwierciedlenie w pliku, dlatego skomplikowane modele zabierają wiele kilobajtów na dysku komputera. W przypadku Generative Components (ale również Grasshoppera) na dysku zapamiętywany jest nie tyle model graficzny, ile scenariusz jego powstawania – skrypt kolejnych kroków budowania. Dlatego w obu programach zapis na dysku to plik o niewielkim rozmiarze. Rozumieją to użytkownicy GH, który na koniec pracy „osadzają” (bake) wykreowany model w środowisku Rhino. Niewielki model w GH (na dysku) zajmuje wiele kilobajtów po „osadzeniu” w Rhino. Osadzony model traci wówczas swój parametryczny charakter, a staje się jedną z wersji modelu GH. W Generative Components jest pozornie podobnie, lecz z punktu widzenia użytkownika działanie polega na wyborze formatu pliku, w jakim model zapamiętujemy na dysku: albo w natywnym formacie GCT (wówczas zapisujemy scenariusz), albo w dowolnym z wybranych, w tym, np. DWG – wówczas zapamiętywana jest geometria, ale tracimy zdolność parametrycznego kontrolowania modelu. Najciekawiej wygląda to przy zapisaniu do natywnej postaci Microstation, czyli DGN. Otóż ten format zapamiętuje obiekty w taki sposób, w jaki powstały: modelowane geometrycznie jako geometryczne, modelowane parametrycznie jako parametryczne. Koegzystencja obiektów w wirtualnej przestrzeni programu jest taka, że dopiero kliknąwszy na obiekt, rozpoznajemy, czy został zdefiniowany parametrycznie. To wielki plus dla GC i moim zdaniem firma McNeel powinna pomyśleć o słabych stronach techniki tzw. „bejkowania” obiektów.
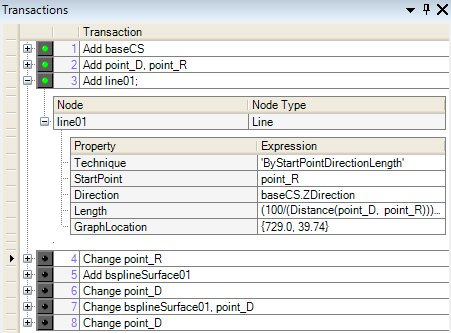
Warto podkreślić również, co w filozofii GC oznacza zapamiętywanie scenariusza. Otóż każda czynność wykonywana przez użytkownika jest lub może być (podkreślam: może) zapisana w tzw. transakcjach – transactions (rys. 1). Zawsze zapamiętywana jest każda czynność związania z postępami w budowaniu modelu – dodanie punktu lub zdefiniowanie powierzchni. Ale poszczególne transakcje (czytaj: kroki postępowania) mogą być w dowolnym miejscu edytowane i zapamiętane (np. przesunięcie punktu), o ile użytkownik ich świadomie nie usunie – a wówczas punkt pozostanie w nowym położeniu, tak jakby był tam „pierwotnie”. Ta filozofia umożliwia wielokrotne, eksperymentalne modyfikowanie zawartości Expressions, czyli właśnie tam, gdzie zwykle umieszczamy sparametryzowaną informację. To użytkownik decyduje, którą z postaci wyrażenia i czy więcej niż jedną warto zapamiętać w scenariuszu postępowania. To istotna zaleta GC. Można zapamiętać każdy wykonany krok i zapisać wszystkie decyzje, które podejmowano przy budowaniu modelu, albo usunąć te, które miały charakter tymczasowy, były jedynie „próbą”. Przykład. Budując linię możemy pierwotnie zdefiniować jej długość jako konkretną liczbę, a następnie zamienić na funkcję. Manipulując transakcjami, decydujemy, czy o tej zmianie pamiętamy w scenariuszu, czy też zapamiętujemy ostateczną postać (długość jako funkcję). To dzięki transakcjom ostateczna wersja modelu może powstać albo jako zapis wyłącznie niezbędnych kroków, albo jako zapis wszystkich „prób”, które w międzyczasie wykonaliśmy. Ostateczna forma modelu pozostanie w obu przypadkach taka sama. To niezmiernie istotna cecha, ściśle związana z myśleniem o „celu jaki chcemy osiągnąć”. Niejednokrotnie istotniejszy od efektu końcowego (model) jego różnych postaci (wersje wynikające ze zmiany parametrów) jest sposób dochodzenia do rozwiązania. To właśnie zapisują transakcje.
Kluczowe cechy programu
Z wielu cech Generative Components zasygnalizuję trzy, na które należy zwrócić szczególną uwagę. Stanowią one kwintesencję filozofii programu. Są to:
• definiowanie parametrów w seriach,
• technika replikacji,
• tworzenie własnych komponentów.
O każdej z nich odnajdziemy wiele informacji w podręcznikach użytkownika. Opanowując GC, starajmy się je wykorzystywać, a osiągniemy wiele ciekawych efektów. Tu przedstawię je jako kluczowe etapy budowania dowolnego modelu, na przykładzie ćwiczenia o nazwie: Free Form Tunel, którego autorem jest Axel Kilian (rys. 2).
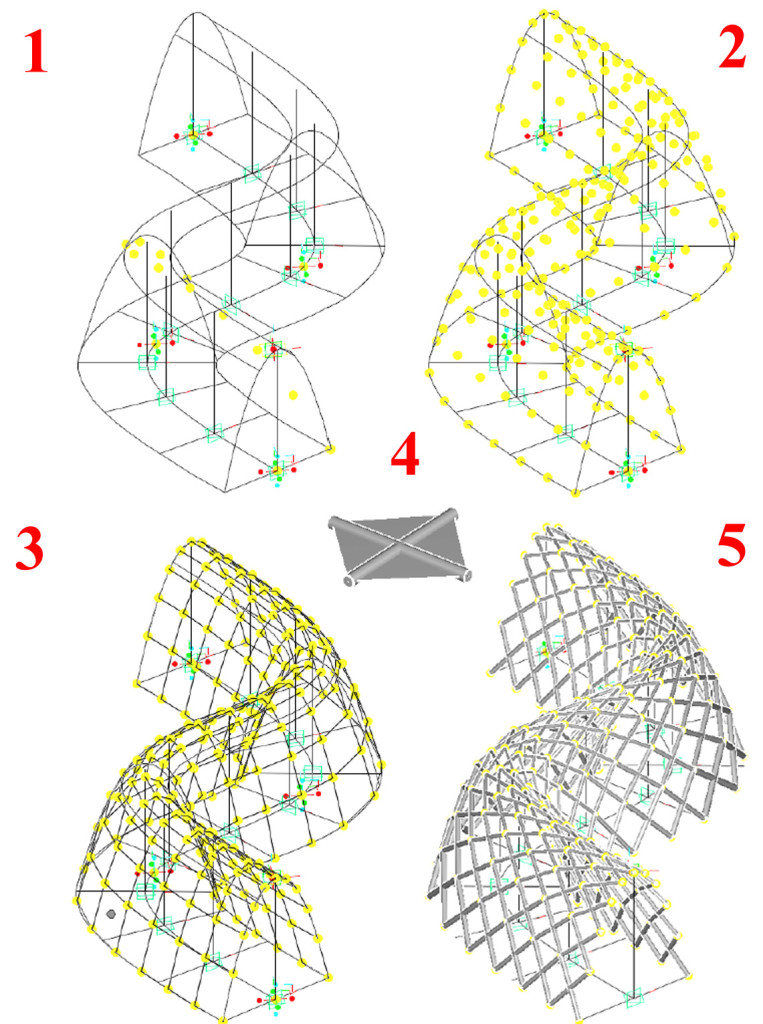
Poniżej istotne etapy pracy.
• Definiowanie parametrów w seriach to nic innego jak narzędzie umożliwiające przedstawienie jednego obiektu w wielu postaciach. Jeden punkt leżący na dowolnej powierzchni może zostać przedstawiony jako seria punktów, np. seria od 0 do 1 co 0.1 wygeneruje 10 równomiernie rozłożonych punktów na całej powierzchni krzywej, natomiast seria od 0 do 0.5 co 0.1 wygeneruje te punkty na połowie powierzchni krzywej (rys. 2, poz. 1).
• Replikacja obiektów to narzędzie generujące całą matrycę na podstawie serii, np. punktów. Zwykle jest używane do pokrycia dowolnej powierzchni chmurą równomiernie rozłożonych punktów. Działanie jest banalne – wystarczy kliknąć na jeden element serii, by uzyskać całą siatkę (rys. 2. poz. 2).
• Równomiernie rozłożona chmura punktów to podstawa tworzenia poligonu, którego poszczególne elementy wyznaczają węzły lokalizacji komponentu reaktywnego (rys. 2, poz. 3).
• Dowolny obiekt zbudowany w GC może zostać zdefiniowany jako własny component reaktywny (rys 2, poz. 4). Reaktywny oznacza zdolność modyfikacji na podstawie zmieniających się parametrów nadrzędnych. W przykładzie narożniki czworokąta mogą przyjmować zadane parametrami współrzędne X, Y, Z.
• Dowolny komponent może stać się powtarzalnym elementem wypełniającym węzły poligonu. Współrzędne siatki poligonu stają się współrzędnymi lokalizacji komponentu (rys. 2, poz. 5).
Przedstawione powyżej etapy prezentują w największym skrócie jedną z podstawowych metod realizacji parametrycznego modelu. Przykład jest prosty, ale chyba nietrudno zauważyć, że ostateczna postać modelu jest zależna od formy komponentu oraz postaci powierzchni krzywej. Manipulując choćby tymi dwoma obiektami, możemy uzyskiwać bardzo ciekawe efekty końcowe. I jeszcze jedno zdanie istotne podkreślenia. Z punktu widzenia filozofii GC tak naprawdę każdy zdefiniowany w modelu obiekt jest komponentem reaktywnym, nawet punkt czy krzywa, ponieważ każdy może reagować na zmieniające jego postać parametry. Powyżej przedstawiliśmy komponent zdefiniowany przez użytkownika, ale pamiętajmy, że wszystkie już zdefiniowane są właśnie reaktywne.
Pierwsze kroki z GC – zadanie do rozwiązania
Przed rozpoczęciem pracy z GC polecam odnalezienie w internecie materiałów, które pomogą w jego opanowaniu. Przede wszystkim należy poszukać pliku o nazwie microstation_GC_v8i_essentials_book. pdf. Ten ponad 300-stronicowy podręcznik zawiera szereg ćwiczeń powszechnie wykorzystywanych w zilustrowaniu cech programu. Wśród nich dwa szczególnie cenne. O jednym już wspomniałem: Free Form Tunel.
Drugie ćwiczenie występuje pod nazwą Simple Form Roof Tree i ilustruje następujący problem: należy na czworokącie zbudować powłokę dachu w taki sposób, aby najwyższy punkt powłoki występował tam, gdzie rośnie drzewo. W dalszej części omówię właśnie to ćwiczenie, ale pamiętać należy, że wskażę jedynie najistotniejsze kroki. Warto odnaleźć wspomniane ćwiczenie np. na YouTube, gdzie wszystkie kroki zostały zapisane w postaci filmu. Kłopot będzie polegał na różnicach w interfejsie użytkownika (znane przykłady opracowano w starszych wersjach). Zaczniemy zatem od instalacji i interfejsu użytkownika, bo jego poznanie musi poprzedzić jakiekolwiek ćwiczenia.
Instalacja i interfejs
Ponieważ nie jest to user manual, ograniczę się jedynie do wskazówek. Jak wspomniałem wyżej, Generative Components występuje w postaci samodzielnej aplikacji oraz jako plug-in do programu Microstation. Jeżeli nie jesteś użytkownikiem Microstation, wystarczy zainstalować wersję stand-alone, choć zainstalowanie Microstation daje dostęp do wielu innych interesujących aplikacji, dla których jest platformą systemową. Jeśli jednak nigdy wcześniej nie używałeś Microstation, zrezygnuj z tej opcji ponieważ szybko pogubisz się odróżnianiu, kiedy kontrolę sprawuje GC, a kiedy Microstation.
Studenci uczelni wyższych rejestrują się, a następnie logują na stronie: http://apps.bentley.com/studentserver
W praktyce każdy przyszły użytkownik oprogramowania Bentley musi się zarejestrować, by uzyskać dostęp do usług i serwisów tej firmy.
Po zainstalowaniu i uruchomieniu programu zetkniemy się z interfejsem użytkownika, któremu należy poświecić chwilę uwagi. W zależności od wersji programu interfejs użytkownika może się różnić znacząco. Również sam użytkownik ma niebagatelny wpływ na układ okien na ekranie. W prezentowanej wersji z rodziny SELECTseries 6 zwraca uwagę przede wszystkim lewa strona ekranu, gdzie do wybory jest najwięcej „opcji”. Po prawej stronie są dwa okna dialogowe reprezentujące to, co realizujemy jako model (rys. 3).
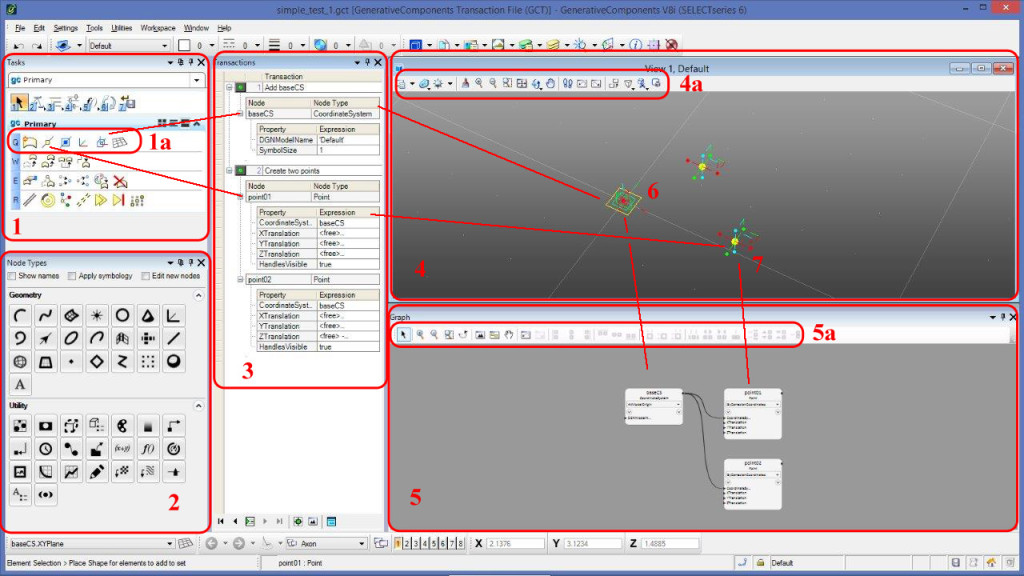
W oknach dialogowych wyświetlane są kolejno:
1 – Tasks: palety poleceń (zadań), jakie daje do dyspozycji GC. Wśród nich do najistotniejszych należą ikony oznaczone 1a – pozwalające na definiowanie w przestrzeni modelu bazowych obiektów inicjujących naszą pracę, np. punktu, płaszczyzny, układu współrzędnych,
2 – Node Types: paleta obiektów i narzędzi, jakie mogą zostać zdefiniowane w modelu. Obiekty geometryczne to wszelkiego rodzaju krzywe i płaszczyzny, a wśród narzędzi odnajdziemy np. definiowanie ustawienia kamery w modelu, ale również funkcji matematycznych możliwych do użycia podczas kreowania obiektów,
3 – Transactions: lista wykonywanych kolejno operacji – scenariusz kroków realizacji modelu. To w istocie swoista reprezentacja skryptu, ale zaprezentowana w taki sposób, że w ułożonych na stosie obiektach możemy zmieniać zawartość ich cech (properties), słowem – modyfikować już zbudowany model,
4 – View: okno dialogowe wyświetlające przestrzeń modelu i obiekty w nim budowane. Widok, sposób generowania obrazu, zbliżenia są kontrolowane za pomocą narzędzi oznaczonych jako 4a,
5 – Graph: okno dialogowe diagramu modelu. Wersja SELECTseries 6 różni się od poprzednich przede wszystkim tym oknem dialogowym. Definiowane przez użytkownika obiekty są nie tylko reprezentowane graficzną postacią komponentów oraz ich wzajemnych powiązań, ale również ich zawartość „wypełniamy” treścią, definiując zarówno metodę tworzenia obiektu, jak i jego cechy – properties. Kontrolę nad oknem sprawujemy za pomocą poleceń 5a.
Musimy zatrzymać się na chwilę przy tych różnicach występujących w poszczególnych wersjach programu GC, ponieważ wiele atrakcyjnych przykładów, podręczników i samouczków przygotowano w poprzednich wersjach i początkujący użytkownik będzie miał kłopot z ich wykorzystaniem.
Pierwsza różnica polega na tym, że w poprzednich wersjach GC nie można było modyfikować metod i cech w oknie Graph. Na ilustracji numerem 6 oznaczono obiekt baseCS – bazowy układ współrzędnych. Od niego rozpoczęto pracę nad modelem. Kroki były następujące: wybór ikony bazowego układu współrzędnych (spośród ikon 1a) spowodował, że zarówno w oknie 4, jak i 5 pojawiała się jego graficzna reprezentacja. Cechy tego obiektu można teraz zmieniać zarówno w oknie 3 – Transactions, jak 4-Graph. Prześledźmy punkt 7. Po wyborze w oknie dialogowym 1a pojawia się w obu oknach graficzna reprezentacja punktu. Dokładne położenie punktu może być teraz modyfikowane na ekranie View (poleceniami: select, move) lub w oknie Transactions w pozycjach XTransaction, YTransaction, ZTransaction, lub w oknie Graph w zawartości komponentu reprezentującego ten właśnie punkt.
Druga różnica polega na zawartości okna 2 – Node Types. Dziś obiekty geometryczne są reprezentowane za pomocą ikon graficznych, a wybór metody definiowania wymaga kliknięcia ikony prawym klawiszem myszki. W poprzednich wersjach obiekt, metoda i cechy były reprezentowane w sposób identyczny jak w oknie Transactions.
Przejdźmy obecnie do istotnych reguł jakimi posługuje się GC. Pierwsza dotyczy na pozór skomplikowanego sposobu graficznej reprezentacji obiektów na ekranie (rys. 4).
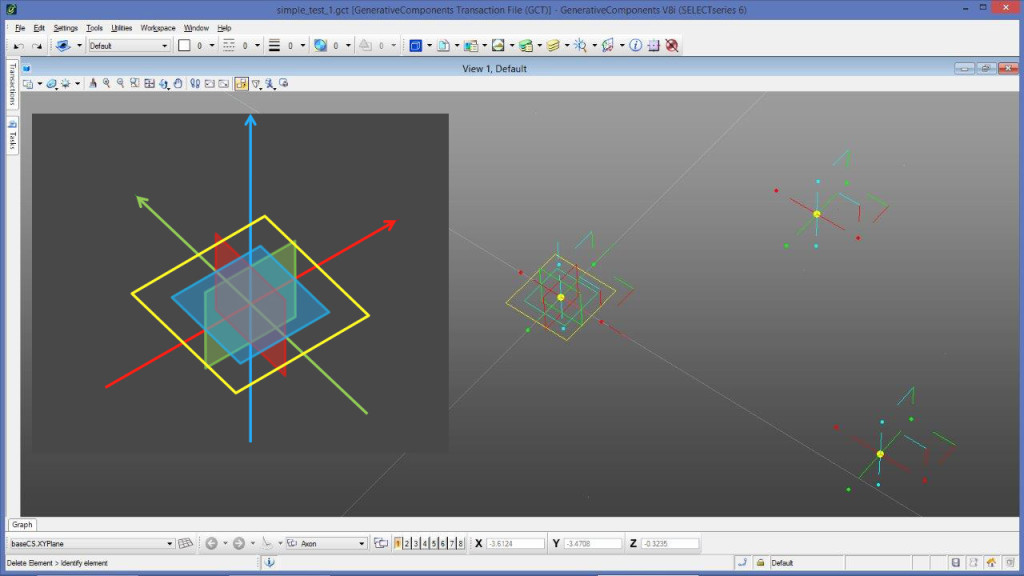
Wyjaśnienie ilustruje schemat po lewej stronie. Zarówno obiekt UCS, jak i punkt są reprezentowane osiami X, Y, Z oraz płaszczyznami XY, XZ, YZ. Przecięcie wszystkich elementów wyznacza współrzędne obiektu, a kolory pomagają w odróżnieniu poszczególnych składowych. Chwytając za te elementy myszką, możemy przesuwać obiekt na ekranie, a wypełniając treścią skrypt lub cechy obiektu możemy zamiast klawiatury kliknąć np. w żółtą płaszczyznę, by system wpisał za nas: plane XY.
Druga cecha CG polega na tym, że w każdym polu definiującym obiekt możemy wpisać niemal dowolną postać informacji, np. zamiast oczekiwanej liczby – funkcję, która tę liczbę wyznacza (rys. 5).

Zilustruję to przykładem, który używa dwóch charakterystycznych narzędzi. Jednym jest funkcja Series, drugim – narzędzie Replication, tworzące automatycznie matrycę wszystkich oczekiwanych wartości (rys. 6).
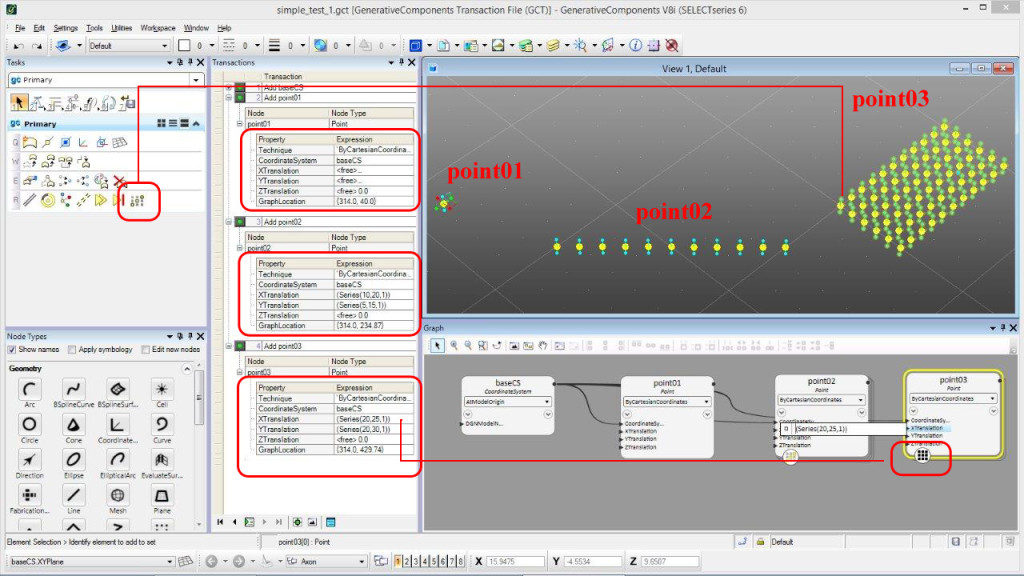
W zależności od wartości zapisanych w polach expressions, graficzna reprezentacja punktu może być skrajnie odmienna. W GC zdefiniowano jedynie 3 punkty.
Na ilustracji widzimy jedynie 3 punkty, ale zostały one zdefiniowane w nieznacznie odmienny sposób. Punkt 01 jest reprezentowany przez współrzędne X, Y, Z (XTransaction, YTransaction, ZTransaction), zdefiniowane kliknięciem myszki na ekranie. W polach tych możemy wpisywać dowolne liczby. Punkt będzie zmieniał swoje położenie, ale graficznie będzie reprezentowany jako jeden punkt. W przypadku punktu 02 posłużono się listą współrzędnych. Taką listę współrzędnych można wpisać ręcznie, np.: {13, 26, 28, 32, 14}, ale podpowiadam, że warto często korzystać z funkcji Series.
Zapis jest następujący: (Series(pierwszy, ostatni, co ile))
Przykłady:
(Series(1,10,1) – zwraca listę {1,2,3,4,5,6,7,8,9,10},
(Series(2,8,2) – zwraca listę {2,4,6,8}.
Punkt02 jest reprezentowany przez dwie serie:
– dla X, od 10 do 200 co 1,
– dla Y od 5 do 15, co 1,
co daje listę 10 punktów o następujących współrzędnych:
{(10,5), (11,6), (12,7), (13,8), (14,9), (15,10), (16,11), (17,12), (18,13), (19,14), (20,15)}.
Jeszcze ciekawiej wygląda punkt03. Po wpisaniu dla X = (Series(20,25,1)) oraz Y = (Series(20,30,1)) naciśnięto ikonę replikacji i wskazano punkt 03. W efekcie punkt 03 jest reprezentowany skończoną matrycą punktów przypisującą każdej współrzędnej X każdą, kolejną współrzędną Y.
Zapamiętajmy te dwa narzędzia, bo są bardzo przydatne w wielu sytuacjach przy budowaniu własnych modeli parametrycznych.
Ćwiczymy na przykładzie
Kilka dodatkowych informacji umożliwi realizację ćwiczenia Simple Form Roof Tree. Ćwiczenie jest polecane do wykonania jako jedno z pierwszych, bo składa się z bardzo niewielkiej liczby kroków, a doskonale ilustruje istotę narzędzia. Zaprezentuję to zadanie w uproszczonej formie, zwracając uwagę na kluczowe elementy. Wspomniałem już, że istotne jest, aby najpierw wyznaczyć cel, a następnie poszukać narzędzi jego realizacji. W prezentowanym ćwiczeniu zadanie polega na rozpięciu na kwadracie powłoki w taki sposób, aby jej najwyższy punkt występował w tym miejscu, gdzie rośnie drzewo. Nie wiemy jednak, gdzie jest ono dokładnie położone wewnątrz kwadratu – może być w dowolnym miejscu. Wyobraźmy sobie zatem kwadrat, a nad nim charakterystyczną powierzchnię. Zamiast drzewa posługujemy się punktem i pionową prostą (rys. 7).
Jak rozwiązać to zadanie? Potrzebujemy dwóch punktów i linii prostopadłej do jednego z nich. Jeden punkt, o nazwie D, będzie reprezentował położenie drzewa, drugi punkt, o nazwie R, będzie reprezentował punkty siatki powłoki. Zależność należy sformułować następująco: kiedy punkt D zbliża się do R, wysokość rośnie.
Lista czynności, które wykonujemy w GC, jest następująca:
1. definiujemy układ współrzędnych,
2. „rysujemy” dwa punkty: D i R,
3. w punkcie R rysujemy prostą L prostopadłą do podstawy (wzdłuż osi Z),
4. długość prostej definiujemy odwrotnie proporcjonalnie do odległości D od R,
5. punkt R zamieniamy na serię punktów R,
6. replikujemy R uzyskując wszystkie warianty,
7. na końcach linii „rozwieszamy” powłokę.
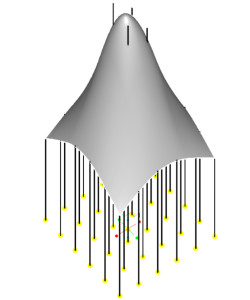
W efekcie tych czynności uzyskamy powłokę, która będzie zmieniać swoją formę w zależności od położenia punku D. Możemy poruszać tym punktem za pomocą myszki lub zmieniać jego współrzędne X, Y. Cały model składa się z pięciu elementów: układu współrzędnych, dwóch punktów, linii i powłoki (rys. 8).
Aby wykonać wymienione powyżej kroki, musimy poznać jeszcze jedną z metod definiowania linii i powierzchni (BSplineSurface) oraz nową funkcję: Distance.
Linię definiujemy metodą: ByStartPointDirectionLength.
Klikamy prawym klawiszem myszki na ikonę linii. Wówczas pojawi się okno dialogowe wszystkich dostępnych metod jej definiowania. Nazwy metod sugerują sposób jej tworzenia. W naszym wypadku musimy wskazać:
– Punkt – Point (point_R),
– Kierunek linii – Direction (baseCS.Zdirection)
– Długość linii – Length (100/(Distance(point_D, point_R))) +0.01)
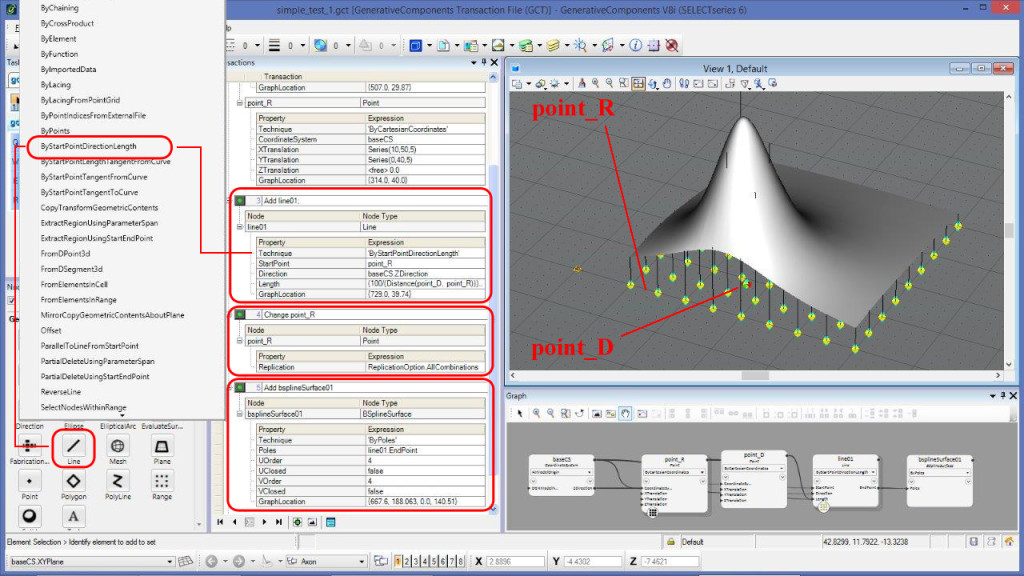
Kierunek linii – pionowo, w górę – to kierunek osi Z. Oś Z jest zdefiniowana przez układ współrzędnych baseCS, stąd poprawny jest zapis: baseCS.ZDirection. Trudniejszy do zrozumienia jest sposób określenia długości linii. To tu zapisany jest warunek „im bliżej punkty R i D, tym dłuższa linia”. Funkcję Distance wykorzystano w taki sposób, że mierzy odległość punktów D i R (Distance(point_D, point_R)). Ale taki zapis dawałby efekt odwrotny od zamierzonego – że im większa odległość punktów, tym dłuższa linia. A ma być odwrotnie, stąd propozycja, aby liczbę, np.: 100, dzielić przez odległość. Dlaczego jednak dodajemy 0.01? Ponieważ gdyby oba punkty leżały dokładnie w tym samym miejscu, to wystąpiłoby dzielenie przez 0.
Zatem zapis długości: (100/(Distance(point_D, point_R))) +0.01) daje w efekcie zamierzony efekt. Tu można pozwolić sobie na wiele eksperymentów, choćby zamieniając 100 na inną wartość, by zaobserwować, jak to wpływa na długość linii.
Powłokę (BSplineSurfce) definiujemy metodą: ByPoles, a są nimi: line01.EndPoint.
Pointa jest następująca. Ponieważ punkt R występuje jako seria punktów, to linia 01 występuje również jako seria linii. Każdy z elementów serii jest w innej odległości od punktu D. Powłoka rozpięta na końcowych punkach linii daje w rezultacie efekt jak na rysunku 7.
Na zakończenie
Przedstawiłem w największym skrócie ćwiczenie: Simple Form Roof Tree. Jako następne polecam wspomniane już Free Form Tunel. Opanowanie obu pozwoli uruchomić wyobraźnię i wykreować własną strukturę. Jeżeli dodatkowo opanowaliśmy techniki wizualizacji, to w ciągu kilku dni jesteśmy w stanie osiągnąć całkiem interesujące efekty, jak ten zrealizowany na zajęciach z parametrycznego projektowania w ramach studiów II stopnia Architecture for Society of Knowledge (rys. 9).

mgr inż. Sławomir Kowal
Wydział Architektury Politechnika Warszawska


















